How to calculate moment of intertia of a rectangle

To calculate the moment of inertia of a rectangle, you need to know its dimensions and the axis of rotation. The moment of inertia measures an object's resistance to rotational motion about a specific axis. For a rectangle, there are two main axes of rotation: one passing through the center of mass (centroid) and parallel to its sides (I_x), and the other perpendicular to the sides and passing through the center of mass (I_y).
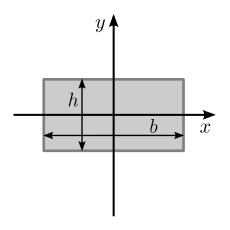
The formulas for calculating the moment of inertia of a rectangle about these two axes are as follows:
-
Moment of Inertia about the x-axis (I_x): I_x = (1/12) * m * (h^2 + b^2)
-
Moment of Inertia about the y-axis (I_y): I_y = (1/12) * m * (b^2 + h^2)
Where:
m = mass of the rectangle
h = height of the rectangle (distance between the parallel sides)
b = width of the rectangle (distance between the perpendicular sides)
You can also calculate the moment of inertia for a rectangle with our free moment of inertia calculator.
If you are dealing with a thin rectangular plate and want to calculate the moment of inertia per unit length, you can divide the above formulas by the length (L) of the rectangle:
-
Moment of Inertia per unit length about the x-axis (I_x): I_x = (1/12) * (h^2 + b^2) * (b/L)
-
Moment of Inertia per unit length about the y-axis (I_y): I_y = (1/12) * (b^2 + h^2) * (h/L)
Remember to use consistent units for the dimensions (e.g., meters) and ensure that the axis of rotation is perpendicular to the plane of the rectangle.