Free Beam Calculator
Calculate bending moment, shear force, deflection & reaction forces for cantilever & simply supported beam.
What's this calculator used for?
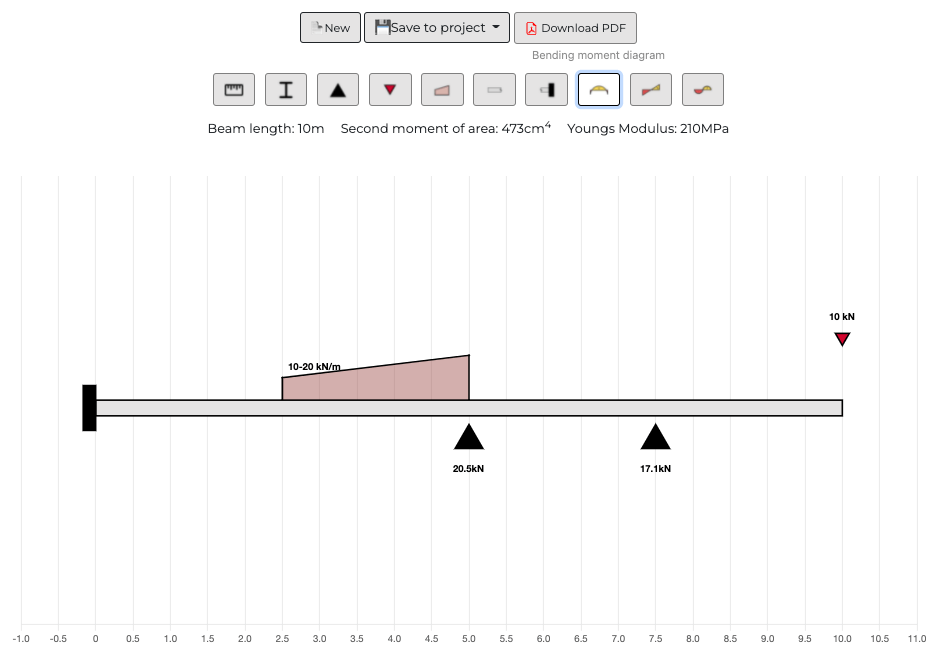
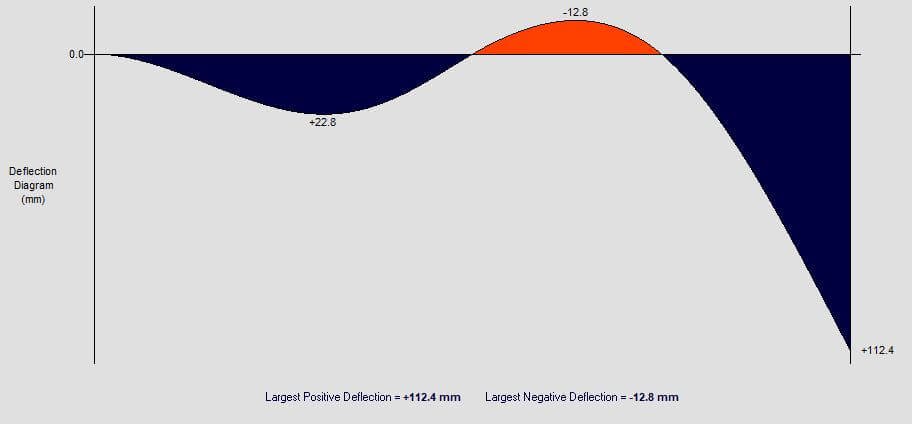
Free online beam calculator to draw bending moment diagrams, shear force diagrams, calculate reaction forces and measure deflection for an indeterminate beam span. This calculator can be used for structural analysis and beam analysis. Maximum bending moment can be calculated along with shear forces, reaction forces and deflection using steel section properties. Specify beam geometry and point loads or distributed loads to get started analysing the beam.
Contribute to this open-source code
This code is open source and you can contribute to it's development.
You can find the source code on GitHub here: IndeterminateBeam
Special credits: Jesse Bonanno
Interested in learning more about automation?

Enroll on our training certifications and learn how to code, build AI applications with no-code tools and automate tasks.
Update beam length
m
Edit beam section
Steel section category:
Universal
Beams
Universal
Columns
European
Beams
European
Columns
American
Beams
SHS
(Square)
RHS
(Rectangle)
CHS
(Circle)
Select a steel section classification:
Section:
Moment of intertia
cm4
Youngs modulus
GPa
Beam weight
kg/m
Check weight is > 0
Edit beam supports
Support number:
Position
mm
Stiffness
kN/mm
Edit point loads
Point load number:
Position
mm
Magnitude
kN
Edit distributed loads
Distributed load number:
From
mm
To
mm
kN/m
kN/m
Distributed Loads
Beam design theory
What is beam stress and how do I calculate beam stress?
When we apply a force somewhere along the span of a beam, we generate internal stresses. There are two types of stress which are generated:
- Normal stress: Generated from forces act along the length of the beam in compression or tension.
- Shear stress: Generated from forces act parallel to the direction of the load.
The origin of these two stress components can be seperated into two force components we refer to as Bending moment and Shear force.
Types of external loading
The simplest loads applied to a beam can be divided into three categories:
- Point loads: This is a force applied to a single point on the beam.
- Distributed loads: This force is distributed over a certain length and acts as a form of pressure.
- Concentrated moment: This is a pure moment acting on a beam at a given position.
Types of support
The simplest supports provided to a beam can be divided into three categories:
- Pinned support: Restrain the beam in both horizontal and vertical directions without providing any restraint against rotation.
- Roller support: Support provided to the beam in only a single direction and no restraint against bending or rotation.
- Fixed support: These supports provide restraint to the beam in all directions and restrain against rotation.
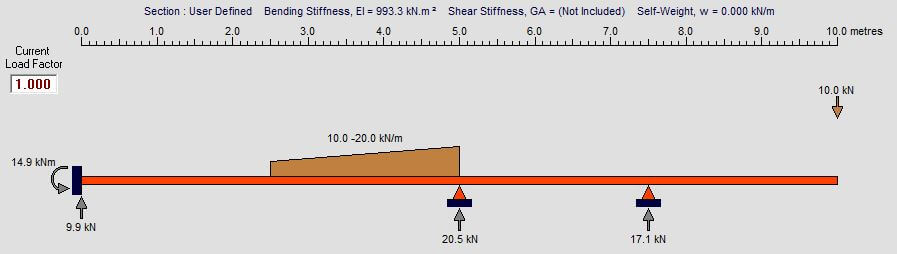
Free body force diagram
To find the forces acting on a beam we must follow the process of creating a free body force diagram.
How to calculate support reaction forces on a beam span?
We first draw the beam to scale indicating the force components of the applied loads and then calculate the support reaction forces.
To calculate reactions we must use equilibrium equations to resolve the external forces:
- Σ Vertical forces applied = 0kN
- Σ Horizontal forces applied = 0kN
- Σ Moments applied = 0kNm
There are two types of cases when resolving beam external conditions:
- Statically determinate: Where the number of equations is equal to the number of unknowns and the calculations can be solved using closed form hand calculations.
- Statically indeterminate: Where the number of unknowns exceeds the number of equations and more advanced methods such as Moment Resistribution Theory need to be used.
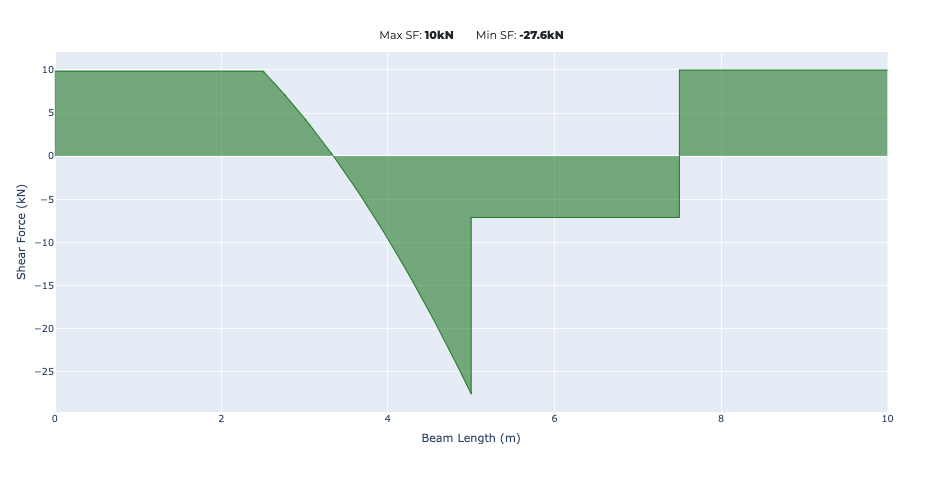
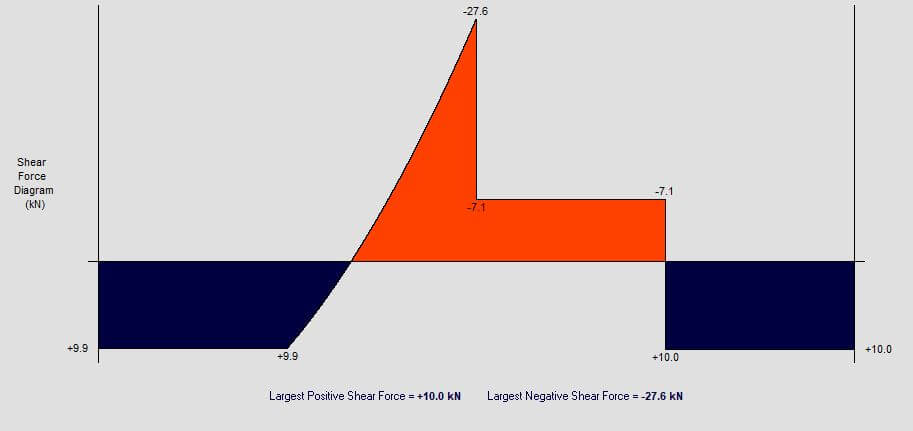
How to draw the shear force diagram?
To create a shear force diagram you work from left to right across the beam summing the applied forces and reactions at each point they are applied. Cantilevers are the most straightforward example of this with a single reaction at one end of the beam span with zero shear force at the unsupported end.
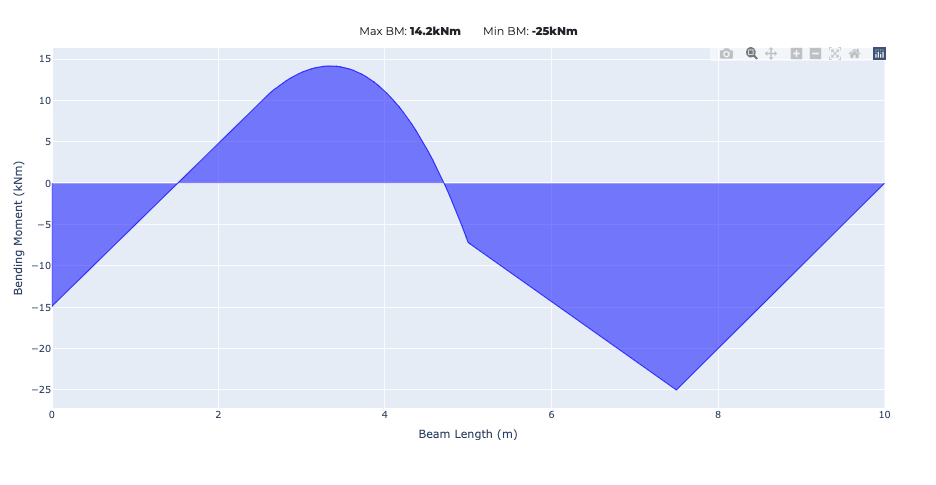
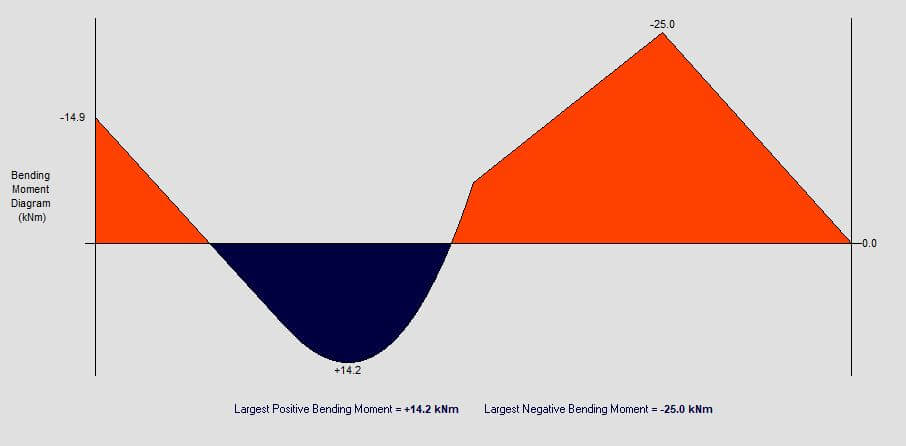
How to draw the bending moment diagram?
To create a bending moment diagram you again must work from left to right across the beam and calculate the moment left of each point you are interested in.